caelestia's math center

CW complexes part 1

Today’s goal is to define CW complexes as the result of certain gluing procedure and deduce some point-set topological properties. This part roughly follows Shastri, Ch2.

Definition 1. Fix $k\geq 1$. Given a topological space $X$ and a family of maps $f_i:S^{k-1}\to X$, $i\in I$, by attaching $k$-cells to $X$, we mean the pushout diagram

Based on the last post, we immediately get

• $X$ is a closed subset of $Y$, and
• Let $\phi_i$ be the right map restricted to the $i$-th disk. These are sometimes called the characteristic maps. Then each open cell in $Y$, defined as $\phi_i(\operatorname{int}D^k)$, is homeomorphic to $\operatorname{int}(D^k)$ via $\phi_i$.
• However, in general a closed cell $\operatorname{im}(\phi_i)$, denoted as $e_i$, need not be homeomorphic to a disk.

Lemma 2. We have

1. A subset $A\subset Y$ is closed iff $A\cap X$ is closed in $X$ and every $A\cap e_i$ is closed in $e_i$.
2. If $X$ is Hausdorff, then the closed cells are closed in $Y$.

Proof. The ‘only if’ is trivial as $X$, $e_i$’s are subsets. To see the other direction, notice that $A\cap e_i$ is closed in $e_i$ implies $\phi_i^{-1}(A)$ is closed in $D^k$, then use that $Y$ is a quotient space.

Part 2. follows from 1, and

\[X\cap e_i=\operatorname{im}(f_i),\]

a slight variation of the equation in the last post.

The following argument depicts the similarity of $Y$ and $X$.

For a subset $B\subset S^{k-1}$, we define

\[N_\varepsilon(B):=\{x\in D^k:\vert x\vert>\varepsilon\,\wedge\,\frac{x}{\vert x\vert}\in B\},\]

where $\varepsilon\in(0,1)$. This extends $B$ into $D^k$ in a consistent manner.

Applying this construction on $X$, we choose any function $\varepsilon:I\to(0,1)$. Given any subset $A\subset X$, put

\[N_\varepsilon(A):=A\cup\bigcup_{i\in I}\phi_i\circ N_{\varepsilon(i)}\circ\phi_i^{-1}(A).\]

Clearly,

• $N_\varepsilon(A)\cap X=A$.
• $N_\varepsilon(A)\cap N_\varepsilon(B)=N_\varepsilon(A\cap B)$, for two subsets $A$, $B$.
• $N_\varepsilon(A)$ is open in $Y$ iff $A$ is open in $X$.
• $A$ is a SDR of $N_\varepsilon(A)$.

We derive that

Theorem 3. If $X$ is T1, T2 or T4, then $Y$ has this property as well.

Proof. The statement about T1 and T2 is easy, by just listing the cases. Fix $a\neq b$ be different points in $Y$. We have

Case 1. Both are in $X$. Pick the separating neighborhood(s) in $X$ and use $N_\varepsilon$ to extend them to open subset(s) of $Y$. The choice of $\varepsilon$ is irrelevant.

Case 2. $a\in X$ and $b$ lies in the $i$-th open cell. By demanding $\varepsilon(i)>\vert\phi_i^{-1}(b)\vert$, the entire $N_\varepsilon(X)$ will be disjoint from a neighborhood of $b$ in the open cell.

Case 3. $a$, $b$ both lie in the open cells. This is trivial, and we have proven the first part.

Now fix disjoint closed subsets $A$, $B$ of $Y$. By T4, there are open sets $U$ and $V$ in $X$ separating $A\cap X$ and $B\cap X$; shrink them so that $\overline{U}\cap\overline{V}=\varnothing$. Define

\[\varepsilon(i)=1-\frac{1}{2}d(\phi_i^{-1}(A\cup\overline{U}),\phi_i^{-1}(B\cup\overline{V})),\]

where $d$ stands for the standard metric, applied to closed subsets of $D^k$. If either subset is empty, we may choose any $\varepsilon(i)$.

The point of this is we want disjoint (which can be directly checked) closed subsets of $Y$,

\[A':=A\cup\overline{N_\varepsilon(U)},\quad B':=B\cup\overline{N_\varepsilon(V)}.\]

Since each open cell is normal, there are disjoint open subsets $U_i$, $V_i$ of $\phi_i(\operatorname{int}D^k)$, and hence of $Y$, such that

\[A'\cap\phi_i(\operatorname{int}D^k)\subset U_i,\quad B'\cap\phi_i(\operatorname{int}D^k)\subset V_i.\]

Finally, we obtain open subsets in $Y$

\[N_\varepsilon(U)\cup\bigcup_{i\in I}U_i,\quad N_\varepsilon(V)\cup\bigcup_{i\in I}V_i,\]

separating $A$ and $B$.

An alternative, cleaner proof of the statements regarding T1 and T4 is covered in the last post.

Theorem 4. Suppose $X$ is T2. Fix an open cover $\{U_j\}_{j\in J}$ of $Y$. Given a partition of unity $\{f_j\}$ subordinate to $\{U_j\cap X\}$ in $X$, there is a partition of unity subordinate to $\{U_j\}$ extending $\{f_j\}$.

For a techinical purpose in Theorem 6, we additionally ask that

• If $f_j$ is zero on an open subset $V$ of $X$, then there is an open $V’\subset Y$ containing $V$, on which the extension of $f_j$ is also zero.

In particular, if $X$ is paracompact Hausdorff, then so is $Y$.

Proof. The plan is to prove this for each closed cell $e_i$ and glue the results together.

Note that $e_i$ is compact. So we can pick some partition of unity $\{g_j\}$ subordinate to $\{U_j\cap e_i\}$. We modify it with the following recipe:

• First, notice that only a finite number of $f_j$ are nonzero on $\phi_i(S^{k-1})$ since it is compact. Denote this finite subset of indeces as $J_0\subset J$.

• Collect the corresponding $U_j$’s, and denote their union by $U$. Then $U$ is an open neighborhood of $\phi_i(S^{k-1})$. Pick $\varepsilon(i)\in(0,1)$ small enough so that

\[T_j:=\overline{N_{\varepsilon(i)}(\{f_j\neq 0\})}\subset U_j,\quad\forall j\in J_0.\]

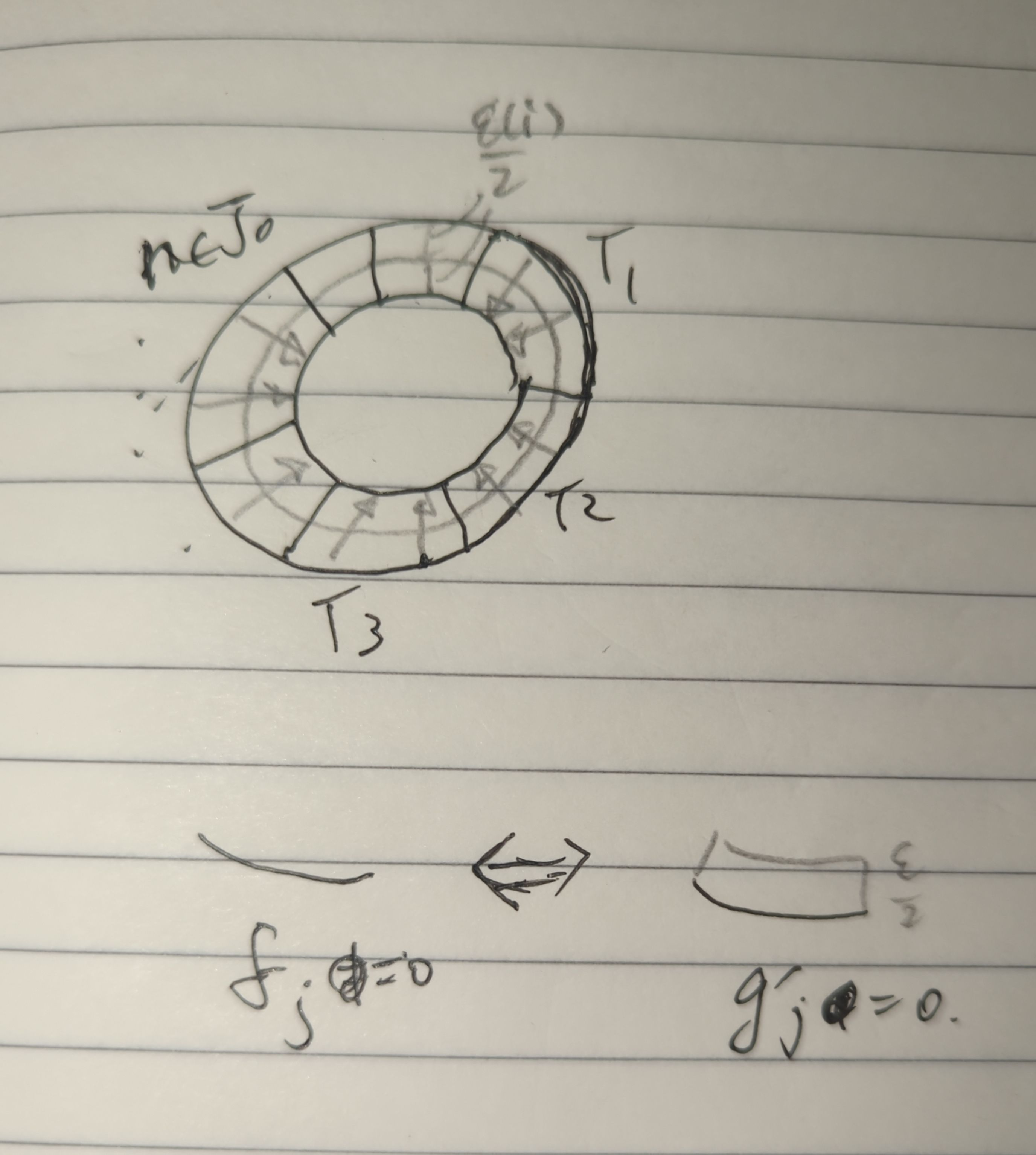
• Pick a function $\theta$ that is nowhere vanishing in the “lessened” open cell $\phi_i(B(0,\varepsilon(i)/2))$ and is zero everywhere else. This is to ensure $g_j$’s play no role at the boundary of the cell. (See the unhelpful figure below.)

• Case 1. If $f_j= 0$ on $\phi_i(S^{k-1})$, i.e. $j\notin J_0$, simply take

\[g'_j:=\theta\cdot g_j.\]

• Case 2. Otherwise, pick a function $\eta_j$ which is $1$ on $T_j$ and has support in $U_j$. Naturally extend $f_j$ to a map

\[\widetilde{f}_j(r):=\vert\phi_i^{-1}(r)\vert\cdot f_j\circ\phi_i\left(\frac{\phi_i^{-1}(r)}{\vert\phi_i^{-1}(r)\vert}\right),\quad r\in e_i.\]

• Then put

\[g'_j:=\theta\cdot g_j+\eta_j\cdot\widetilde{f}_j.\]

• This clearly has support in $U_j$ and extends $f_j$ on $\phi_i(S^{k-1})$. At points inside the lessened open cell, this is nonzero if $g_j$ is; elsewhere (i.e. the “annulus”), it is nonzero iff after “pushing to the boundary”, $f_j\neq 0$.

Since we only increased finitely many $g_j$’s, the result still satisfy the locally finite condition. We can directly see that $\sum_{j}g’_j$ is nowhere vanishing by construction. Therefore $\{g’_j\}$ is a partition of unity extending $\{f_j\}$ to $e_i$.

Finally, we can glue these local results together to get the desired extension of $\{f_j\}$. The sum is clearly nonvanishing. The locally finiteness inside the open cells is trivial. We just need to check that on $X$. We just need the following observation.

• If $f_j$ is zero on an open subset $V$ of $X$, then the extension of $f_j$ is zero on $N_{\varepsilon/2}(V)$.

We have defined each $\varepsilon(i)/2$ above; we know $N_{\varepsilon/2}(V)$ is open in $Y$; finally, this claim follows from the last clause in the above discussion.

We are now ready to give the following definition.

Definition. A CW complex is a space $X$, together with a sequence of subsets $\{X^{(n)}:n\geq 0\}$ called the $n$-th skeleta of $X$, satisfying

1. $X^{(0)}$ is a discrete space.
2. $X^{(n)}$ is obtained by attaching $n$-cells to $X^{(n-1)}$, for all $n\geq 1$.
3. $X=\bigcup_{n\geq 0}X^{(n)}$ is the colimit of the sequence

\[X^{(0)}\subset X^{(1)}\subset \cdots\subset X^{(n)}\subset\cdots\]

The morphisms, called cellular maps, between CW complexes $f:X\to Y$ are continuous maps such that $f(X^{(n)})\subset Y^{(n)}$ for all $n\geq 0$. We thus have a category $\mathsf{CW}$.

Remark. Condition 3 is sometimes states as the topology of $X$ is coherent with its $n$-skeleta, and was once dubbed “the weak topology”. Though I don’t think I’ll use this terminology here.

Proposition 5. Fix a CW complex $X$. We have

1. A subset $A\subset X$ is closed iff $A\cap X^{(n)}$ is closed in $X^{(n)}$ for all $n\geq 0$.
2. A subset $A\subset X$ is closed iff $A\cap e$ is closed in each closed cell $e$.
3. The $n$-skeleton $X^{(n)}$ is closed in $X$.
4. Each closed cell $e$ is closed in $X$.
5. $X$ is compactly generated and Hausdorff.
6. The closure of the $i$-th open cell $\epsilon_i$ is $e_i$

Note that the open cells need not be open in $X$.

Proof. 1 is the definition of the topology of the union. 2 is a combination of 1 and induction with Lemma 2.1.

3 follows from 1 and the simple fact that $X^{(n)}$ is a closed subset of $X^{(m)}$ for $n\leq m$.

Since each skeleton is Hausdorff by Theorem 3, so is $X$. Thus the closed cells are closed as images of compact disks. This proves 4 and 5.

$\overline{\epsilon_i}\subset e_i$ follows from 4 and $e_i\subset\overline{\epsilon_i}$ follow from continuity of $\phi_i$.

Theorem 6. $X$ is paracompact.

Now we prove 6. Fix an open cover $\{U_j\}_{j\in J}$ of $X$. We inductively give a partition of unity subordinate to $\{U_j\cap X^{(n)}\}$ for all $n\geq 0$.

If $n=0$, we pick a well-ordering on $J$, and take $f_j^{(0)}(x)=1$ if $U_j$ is the first that contains $x$ and $0$ otherwise. This is clearly a partition of unity on $X^{(0)}$. The inductive step is provided by Theorem 4.

It is now clear why we need that additional condition in Theorem 4. It makes sure after we glue everything together:

\[f_j:=\bigcup_{n\geq 0}f_j^{(n)},\]

the resulting $\{f_j\}$ still satisfy the locally finite condition, and is thus a partition of unity.

A few examples of CW complexes:

• A graph is a $1$-dimensional CW complex, i.e. $X=X^{(1)}$.

• A subcomplex $Y$ of $X$ is a subspace with a CW complex structure, such that every cell in $Y$ is also a cell in $X$, in the sense that they have the same characteristic map. Trivially, $X^{(n)}$ is a subcompex of $X$. A more useful characterization is given in Theorem 9.

• $\mathbb{R}^n$ is an $n$-dimensional CW complex for any $n$. The $0$-th skeleton is the lattice $\mathbb{Z}^n$, $1$-cells are line segments connecting adjacent points, $2$-cells are faces, and so on. To see that what we get is indeed $\mathbb{R}^n$, simply notice that the closed cells form a locally finite closed cover of $\mathbb{R}^n$.

• Then $\mathbb{R}^n$ is a subcomplex of $\mathbb{R}^m$ if $n\leq m$. We can thus take the colimit of \(\mathbb{R}^0\subset\mathbb{R}^1\subset\cdots\subset\mathbb{R}^n\subset\cdots\)

This endows $\mathbb{R}^\infty$ a CW complex structure. However, this topology is finer than the topology induced by the norm.

• $S^n$ can be constructed as the unique CW complex with one $0$-cell and one $n$-cell.

• However, this does not make $S^n$ a subcomplex of $S^m$. To achieve this we need the more standard setup: $S^{n+1}$ is obtained by attaching two $n+1$-cells, i.e. the upper and lower hemispheres, to $S^n$, i.e. the equator.

• We then have $S^\infty$, as above. This is a subspace of $\mathbb{R}^\infty$.

• $\mathbb{R}P^{n+1}$ is obtained by attaching one $n+1$-cell to $\mathbb{R}P^n$ along the double cover. And thus we have $\mathbb{R}P^\infty$.

• $\mathbb{C}P^{n+1}$ is obtained by attaching one $2n+2$-cell to $\mathbb{C}P^n$ along the Hopf fibration $\pi:S^{2n+1}\to\mathbb{C}P^n$. And thus we have $\mathbb{C}P^\infty$.

Lemma 6. As a set, a CW complex is the disjoint union of its open cells.

Proof. Obvious.

Proposition 7. A subset $A\subset X$ is discrete and closed iff its intersection with each open cell is finite.

Proof. If $A$ is discrete and closed, its intersection with each closed cell is discrete and compact, hence finite.

Now suppose $A$ has finite intersection with each open cell. Induction shows that $A\cap X^{(n)}$ is closed for all $n$. When $n=0$ there’s nothing to prove. Given $A\cap X^{(n-1)}$ is closed, the intersection of $A$ with each closed $n$-cell is the union of a closed subset and finitely many points, hence closed. Therefore $A\cap X^{(n)}$ is closed by Lemma 2.1.

We conclude that $A$ is closed in $X$ by Proposition 5.1. Since the same is true for any subset of $A$, $A$ is discrete.

Theorem 7.(Closure finiteness) Every compact subset $K$ of $X$ is contained in finitely many open cells.

Proof. Choose a point $x_i$ from each open cell $\epsilon_i$ that intersects $K$. Then apply Proposition 7 to $\{x_i\}$.

Corollary 8.(Closure finiteness’) Every compact subset $K$ of $X$ is contained in a finite subcomplex $Y$, i.e. a subcomplex with finitely many cells.

Proof. It suffices to show this for every single closed cell $K=e_i^n$. But then $\phi_i(S^{n-1})$ is compact and is contained in $X^{(n-1)}$. By recursion, we are through.

Theorem 9. Let $Y$ be a subspace of the CW complex $X$. TFAE

1. $Y$ is a subcomplex of $X$.
2. $Y$ is closed and is (as a set) a union of some open cells of $X$.
3. $Y$ is (as a set) a union of some open cells of $X$, and if $\epsilon_i\subset Y$ then $e_i\subset Y$.

Proof. 1 $\Longrightarrow$ 2: Suppose that $Y$ is a subcomplex of $X$. Then $Y$ is a union of open cells in $Y$ which are also open cells in $X$. To prove that $Y$ is closed, we inductively show that $Y\cap X^{(n)}=Y^{(n)}$ is closed. Indeed, $Y^{(n)}$ is the union of $Y^{(n-1)}$ and some open $n$-cells, so is closed in $X^{(n)}$ by Lemma 2.1.

2 $\Longrightarrow$ 3 is trivial. Now we prove 3 $\Longrightarrow$ 1:

Define $Y^{(n)}$ in the evident way. We inductively show that $Y^{(n)}$ is a subcomplex of $X$. When $n=0$ there’s nothing to prove. By induction hypothesis and the direction above, $Y^{(n-1)}$ is closed in $X$.

So, if $U\subset Y^{(n)}$ intersects $Y^{(n-1)}$ in a closed subset of $Y^{(n-1)}$, then $U\cap Y^{(n-1)}$ is closed in $X$. Thus $U\cap Y^{(n-1)}\cap e_i$ is closed in $e_i$ for every closed $n$-cell of $X$. If moreover $U$ intersects every closed $n$-cell in $Y$ in a closed subset, then $U$ intersects every $e_i$ in a closed subset. So $U$ is closed in $X$. Therefore, $Y^{(n)}$ with the subspace topology is obtained by attaching $n$-cells to $Y^{(n-1)}$.

To conclude that $Y$ is a subcomplex, we need that the subspace toplogy on $Y$ agrees with $\varinjlim_n Y^{(n)}$. Suppose $U\subset Y$ satisfies $U\cap Y^{(n)}$ is closed for all $n\geq 0$. For every open cell $\epsilon_i$ in $X$,

• Case 1. $\epsilon_i\subset Y$, so $e_i\subset Y$ as well. By closure finiteness and Lemma 6, $e_i\subset Y^{(m)}$ for some $m$. Therefore

\[U\cap e_i=U\cap e_i\cap Y^{(m)}\overset{\text{closed}}\subset e_i.\]

• Case 2. $\epsilon_i\cap Y=\varnothing$. Again by closure finiteness, only a finite number of open cells in $Y$ intersects $e_i\setminus\epsilon_i$, denoted as $\alpha_1$, $\alpha_2$, $\cdots$, $\alpha_k$. Then

\[U\cap e_i=U\cap e_i\setminus\epsilon_i=U\cap(\overline{\alpha_1}\cup\overline{\alpha_2}\cup\cdots\cup\overline{\alpha_k})\cap e_i.\]

By case 1, each $U\cap\overline{\alpha}\cap e_i$ is closed. As a finite union of closed subsets, $U\cap e_i$ is also closed. We hence deduce that $U$ is closed in $X$.

Corollary 10. The arbitrary union or itersection of subcomplexes is itself a subcomplex.

---

Post date: 2025/02/27
Home page